জেটা ফাংশন

Rieman zeta ফাংশন ζ(z) ডোমেইন কালারিং দিয়ে প্লট করা হয়েছে।

$z=1$-এ মেরু এবং গুরুত্বপূর্ণ লাইনে দুটি শূন্য।

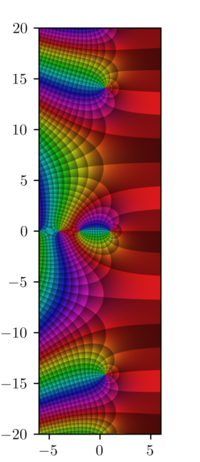
'রিম্যান জেটা ফাংশন' বা ''ইউলার–রিম্যান জেটা ফাংশন", যাকে গ্রিক অক্ষর ζ (zeta) দ্বারা চিহ্নিত করা হয় থাকে তা একটি জটিল চলক এর একটি গাণিতিক ফাংশন যাকে $$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots$$ ধারাটি দ্বারা $\operatorname {Re} (s)>1$, এর জন্য সংজ্ঞায়িত করা হয় এবং এর বিশ্লেষণমূলক ধারাবাহিকতা দ্বারা অন্যান্য ডোমেইনে সংজ্ঞায়িত করা হয়৷

Riemann zeta ফাংশন বিশ্লেষণীয় সংখ্যা তত্ত্ব-এ একটি গুরুত্বপূর্ণ ভূমিকা পালন করে, এবং পদার্থবিদ্যা, সম্ভাব্যতা তত্ত্ব, এবং প্রয়োগ পরিসংখ্যান এর প্রয়োগ রয়েছে।

লিওনহার্ড অয়লার অষ্টাদশ শতাব্দীর প্রথমার্ধে বাস্তব এর উপর ফাংশনটি প্রথম প্রবর্তন ও অধ্যয়ন করেন। বার্নহার্ড রিম্যান-এর 1859 প্রবন্ধ "প্রদত্ত মাত্রার চেয়ে কম প্রাইমের সংখ্যার উপর" অয়লার সংজ্ঞাকে একটি জটিল পরিবর্তনশীলে প্রসারিত করেছে, এটির মেরোমরফিক ধারাবাহিকতা প্রমাণ করেছে। এবং কার্যমূলক সমীকরণ, এবং এর [[ফাংশনের মূল এই কাগজটিতে রিম্যান জেটা ফাংশনের জটিল শূন্যের বণ্টন সম্পর্কে রিম্যান হাইপোথিসিস, একটি অনুমান রয়েছে যা অনেক গণিতবিদ বিশুদ্ধ গণিত-এর সবচেয়ে গুরুত্বপূর্ণ অমীমাংসিত সমস্যা বলে মনে করেন।

এমনকি ধনাত্মক পূর্ণসংখ্যাতে রিম্যান জেটা ফাংশনের মান অয়লার দ্বারা গণনা করা হয়েছিল। তাদের মধ্যে প্রথমটি, ζ(2), বেসেল সমস্যার সমাধান প্রদান করে। 1979 সালে Roger Apéry ζ(3) এর অযৌক্তিকতা প্রমাণ করেছিলেন। ঋণাত্মক পূর্ণসংখ্যা বিন্দুতে মানগুলি, অয়লার দ্বারাও পাওয়া যায়, মূলদ সংখ্যাs এবং মডুলার ফর্মs তত্ত্বে গুরুত্বপূর্ণ ভূমিকা পালন করে। রিম্যান জেটা ফাংশনের অনেক সাধারণীকরণ, যেমন ডিরিচলেট সিরিজ, ডিরিচলেট L-ফাংশন এবং L -ফাংশন, পরিচিত।